М.Э. Гусельников, В.Н. Стройнова
Биоэкология
Учебное пособие. – Томск: Изд. ТПУ, 2002. – 104 с.

Предыдущая

Оглавление

Следующая

7. Свойства популяций

Динамика популяций

Популяция представляет собой динамичную, изменяющуюся со временем систему. Меняться могут плотность, рождаемость, выживаемость, численность популяции. Рассмотрим подробно динамику численности популяций. Численность популяции в заданной среде описывается линейным дифференциальным уравнением первого порядка:

где К — постоянный коэффициент рождаемости, p — постоянный коэффициент смертности, N — способность среды поддерживать популяцию (максимально возможная численность популяции). Решение этого уравнения представляет собой функцию

Постоянная интегрирования С определяется из начальных условий:

при t = 0 численность популяции равна Х₀. Рассмотрим два предельных случая:

1. При t → 0        exp → 1,     Х → Х₀.

2. При t → ∞       exp → 0,      Х → (N — р/К).

На графике рис. 7.1 это логистическая кривая.

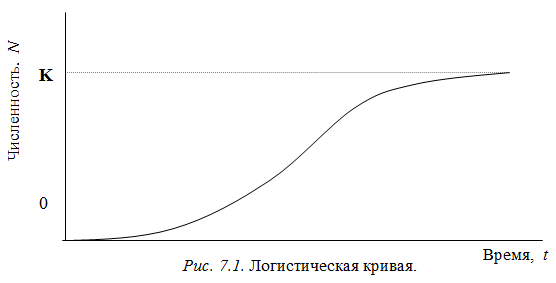
В соответствии с принципом минимального и максимального размера популяции численность не может превышать строго определенной величины (N — р/К) и не может быть меньше величины Х₀. Популяция перестает расти, когда ресурс среды (пища) оказывается исчерпанным. Вспомните принцип конкурентного вытеснения Гаузе. Если решить систему из двух уравнений

получим две логистические кривые.

Из анализа устойчивости решения приведенной системы дифференциальных уравнений следует возможность появление новых видов и вытеснения старых видов (Х₁) новыми (Х₂), если N₂ — p₂ / K₂ > N₁ — P₁ / K₁ . В процессе вытеснения численность Х₁ популяции 1 падает, в то время как численность Х₂ популяции 2 растет. На рис.7.2 показано последовательное заполнение экологической ниши новыми видами.

Таким образом, различные популяции имеют разную динамику численности. Различают три типа динамики численности (рис. 7.3):

I. Стабильная динамика. Характеризуется малой амплитудой колебаний и большим (около 20 лет) периодом. Наблюдается у крупных животных с малой плодовитостью и большой продолжительностью жизни (слоны, киты, приматы, человек).

II. Лабильная динамика. Характеризуется периодом 5-11 лет и большей амплитудой. Наблюдается у крупных птиц, рыб, хищников, грызунов.

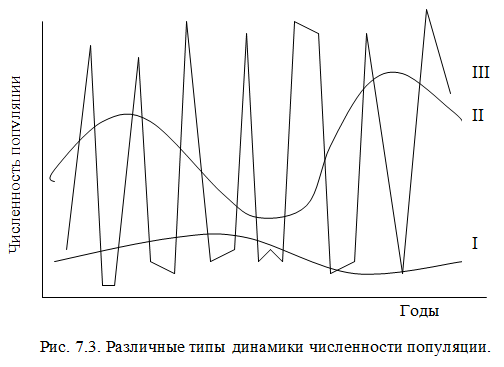
III. Эфемерная динамика. Характеризуется неустойчивостью численности (амплитуда колебаний велика) и малым (4 — 5 лет) периодом колебаний. Наблюдается у мелких грызунов и насекомых.

Иерархия, поведение

Рассмотрим иерархию стада павианов на опасном участке саванны.  Внутри стада идут самцы-иерархи, самки с детенышами и детеныши несамостоятельные. Это самое безопасное место в стаде, одновременно удобное для управления и обозрения. Впереди стада идут самцы второго ранга, это наиболее опасное место. При встрече с хищником самцы второго ранга выстраиваются полумесяцем, стремясь задержать и окружить противника. В это время остальное стадо убегает. Позади и с боков стада идут самцы третьего ранга, охраняя его. Таким образом, выстраивается пехота в предбоевом порядке. Специально выработанная система сигналов позволяет животным найти брачные пары, защитить свою территорию, обеспечить выживание потомства. При территориальных стычках самцы принимают угрожающие позы, издают звуки, метят территорию, но при первых признаках испуга отступают и складывают оружие. То есть самцы внутри стада не уничтожают друг друга, а борются насмерть только с чужаками или хищниками.

Структура популяции, иерархия внутри популяции строго поддерживаются с помощью поведения. Поведение определяется основными принципами биологической морали:

1.  Не бить лежачего.

2.  Не трогать детенышей.

3.  Не покушаться на чужую территорию, чужое гнездо, чужую самку.

4.  Не нападать неожиданно или сзади.

5.  Не отнимать и не воровать пищу.

Таким образом, популяция имеет структуру, изменяющуюся со временем. Меняется также численность популяции, но в определенных пределах. Большое значение имеет характеристика плотности популяции. Если она превышена и не соответствует внешним условиям, то рождаемость падает, а смертность увеличивается. Например, резкое увеличение плотности популяции саранчи или леммингов вызывает их миграцию, и, дойдя до моря, они гибнут. При этом восстанавливается численность и плотность, популяция остается устойчивой. В случае большой скученности наблюдается также частичная гибель от эпидемий и конкурентной борьбы. То есть популяция сама поддерживает свою численность и плотность.

Характеристикой устойчивой популяции является кривая выживания. Внутри популяции осуществляется обмен энергией и веществом (через пищу — молоко у млекопитающих), информацией либо о внешней среде от родителей к детенышам, либо генетической при рождении. Популяция, как любая система, подчиняется системным законам.

Отношения между популяциями

Разные популяции могут взаимодействовать между собой. Вспомните об отношениях в экосистеме: принцип конкурентного исключения Гаузе, парадокс Хатчинсона. Таким образом взаимодействуют популяции одного вида, а также особи внутри одной популяции. Могут быть отношения типа "хищник-жертва", "паразит-хозяин", симбиоз. С помощью этих отношений взаимодействуют популяции разных видов. Все эти отношения регулируют численность различных популяций. Уравнения Лотки — Вольтерры, описывающие численность популяций хищников и их жертв, имеют вид

dx/dt = by;            dy/dt = — bx,

где b — постоянный коэффициент, определяющий степень поддержки со стороны окружающей среды, x(t) — численность популяции жертв, y(t) — численность популяции хищников. В фазовом пространстве x, y решение имеет форму концентрических окружностей. То есть численность взаимодействующих популяций постоянна, популяции устойчивы.

Если перевести уравнения Лотки — Вольтерры в систему координат, связанную со временем (путем дифференцирования обоих уравнений), получим:

d²х / dt² = — b² х,

d²y / dt² = — b² y.

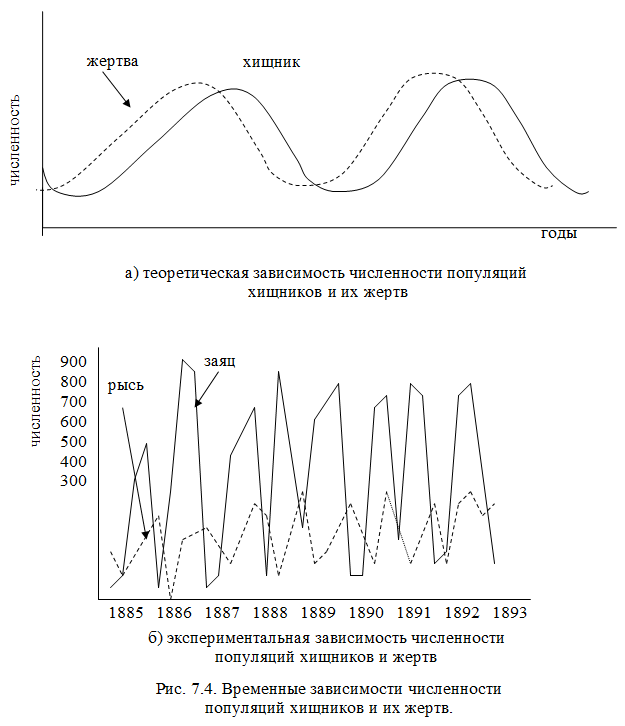
Решением системы уравнений является функция х(t) = exp (-bt) в соответствии с выбранными начальными условиями х = sin(bt), y = cos(bt). То есть численность популяции хищников отстает по фазе на π / 2 от численности жертв. Зависимости x(t), y(t) показаны на рис.7.4: верхняя (а) –

теоретическая и нижняя (б) — реальная.

Следует заметить, что на экспериментальной кривой численность жертв превышает численность хищников. Это находится в полном соответствии с законами экологии (вспомните распределение биомассы по трофическим уровням).

Вольтерра сформулировал три следующих закона взаимодействия популяций хищника и жертвы:

1. Процесс уничтожения жертвы хищником приводит к периодическим колебаниям численности популяций обоих видов; эти колебания зависят только от скорости роста популяций хищника и жертвы и от исходного соотношения их численностей.

2. Средняя численность популяции для каждого вида постоянна независимо от начального уровня при условии, что скорости увеличения численностей и эффективность хищничества постоянны.

3. При нарушении популяций хищника и жертвы в силу внешних причин (например, уменьшение численности рыб в ходе промысла) средняя численность популяции жертвы растет, а популяции хищника падает.

Уравнения Лотки — Вольтерры и законы Вольтерры действуют внутри сообществ, когда взаимодействуют популяции разных видов. Их можно назвать законами сообществ.

Тест

1. Динамика численности популяции людей:

1. Эфемерная.

2. Лабильная.

3. Стабильная.

2. Динамика численности популяции насекомых:

1. Эфемерная.

2. Лабильная.

3. Стабильная.

3. Уравнение первого порядка для определения численности популяции имеет вид:

1. dх/dt = Кх(N-х) — Pх . 

2. dх/dt = Кх(N-х) – Kх.

3. dх/dt = Кх(N-х) – Nх.

4. Принцип конкурентного исключения Гаузе выполняется при условии (вид 2 вытесняет вид 1):

1. N₂ — P₂ / К₂ > N₁ — P₁ / К₁ . 

2. N₂ — P₂ / К₂ < N₁ — P₁ / К_{1 .}

3. N₂ — P₂ / К₂ = N₁ — P₁ / К_1.

5. Связана ли логистическая кривая для популяции с принципом минимального и максимального размера популяции?

1. Да.

2. Нет.

6. Уравнения Лотки — Вольтерры описывают:

1. Совместное изменение численности популяций симбионтов.

2. Совместное изменение численности популяций паразитов и хозяев.

3. Совместное изменение численности популяций хищников и жертв.

7. Численность популяций хищников и их жертв не совпадает во времени:

1. Жертвы опережают хищников.

2. Хищники опережают жертв.

3. Меняются одновременно.

8. Какие характеристики устойчивой популяции постоянны? 1.Численность популяции.

2. Плотность популяции.

Предыдущая

Оглавление

Следующая