С.В. Комонов, Е.Н. Комонова
Ветровая эрозия и пылеподавление
Курс лекций. — Красноярск: Изд-во СФУ, 2008. — 192 с.
| Предыдущая |
Содержание статьи:
Глава 1. Ветровая эрозия
1.8. Методы изучения эрозии грунта
1.8.1. Методология эрозионных исследований
Существуют четыре основных метода:
· сравнительно-географический,
· сравнительно-аналитический,
· стационарный
· моделирование.
Для процессов ветровой эрозии характерно наличие собственного объекта и специфических методов исследований. Объект исследования — совокупность явлений и процессов в биосфере, связанных с механическим движением грунтовой массы под действием воздушных потоков. Поэтому одним из основных методов исследования нового направления является аэромеханический. Специфика этого метода в том, что он предполагает изучение свойств грунта, определяющих их противодефляционную стойкость, потоков воздуха, эродирующего грунта, процессов отрыва, переноса и отложения грунтовых частиц. При изучении эрозии грунта наряду с методами грунтоведения применяются и методы смежных наук, таких, гидравлика, физика атмосферы, ,науки о Земле, грунтоведение и др.
Наибольшие успехи достигнуты с использованием сравнительно-географического и стационарного методов. Дальнейшие перспективы сравнительно-географического метода связаны с развитием дистанционных методов:
· аэро- и космической эрозионной фотосъемки;
· наземной эрозионной съемки с использованием спутниковой системы глобальной навигации, которая позволяет очень точно определять на местности эрозионные объекты.
Стационарные методы остаются наиболее важными в сборе информации, необходимой для познания процессов эрозии и разработки противоэрозионных мероприятий.
Наиболее быстрыми темпами развиваются в настоящее время методы моделирования. Это обусловлено теми преимуществами, которые возникают вследствие замены реального объекта исследования его более простой моделью.
Наиболее широко распространенным видом эрозионных моделей являются почвенно-эрозионные карты. Они относятся к классу так называемых графических моделей, для которых характерна очень высокая степень сжатия информации, обеспечивающая ,возможность анализа эрозионной обстановки на больших территориях.
Особенно характерным для эрозионоведения является использование физических моделей. Это единственный метод познания механизмов взаимодействия водных и воздушных потоков с грунтом, приводящего к ее эрозии. Наибольшей степенью абстрактности отличаются математические модели, которые все более широко применяются во всех отраслях.
Модели эрозии грунта строятся на более или менее полном учете факторов и условий эрозии. В зависимости от масштаба модели бывают:
· локальными,
· регаональными
· глобальными.
Модели также подразделяются на:
· статистические, не вскрывающими физического смысла процесса эрозии,
· логико-математические, основанными на уравнениях, с той или иной степенью точности описывающих влияние разных факторов эрозии.
Логико-математические модели делятся на три класса.
· Модели с сосредоточенными параметрами, т. е. не учитывающие пространственной неоднородности района проявления эрозии или отдельной площади пыления.
· Модели с сосредоточенно-распределенными параметрами, т. е. переходные.
· Модели с распределенными параметрами, основанные на дифференциальных уравнениях в частных производных.
Подавляющее большинство моделей эрозии относится к первому классу. В классе моделей с сосредоточенными параметрами выделяются:
· системные модели типа "черный ящик", т. е. модели, типа "вход — выход";
· системно-физические или концептуальные модели тина "серый ящик", т. е. модели, частично учитывающие физику процессов, частично построенные по типу "черного ящика";
· физические непрерывные модели, т. е. модели целиком построенные на учете физики явления.
В зависимости от степени завершенности можно выделить исследовательские модели
· высокого уровня,
· модели более низкого уровня, но более полные, доведенные до возможности практического использования при планировании мероприятий по охране от ветровой эрозии.
Математические модели являются не только средством познания, но и объектом исследования. В связи с этим, распространяются методы вычислительного эксперимента.
Основу вычислительного эксперимента составляет триада "модель-алгоритм-программа". Создание комплексных моделей все более широко распространяется в связи с увеличением доступности высокопроизводительных ЭВМ. Чаще всего комплексная модель состоит из большого числа простых и комплексных подмоделей, описывающих: погоду, осадки, температуру, солнечную радиацию, ветер, температуру грунта, динамику элементов минерального питания (азота, фосфора), ограничивающие факторы, систему механической обработки, влияние мелиорации (дренаж, орошение, удобрение, известкование, внесение пестицидов, эрозию и др.
Для описания ветровой эрозии в модели используют модифицированные версии "универсального уравнения потерь грунта" и "уравнения ветровой эрозии". Указанная модель имитирует перечисленные процессы с шагом в одни сутки.
Исходя из степени вмешательства исследователя в ход изучаемого процесса все многообразие применяемых экспериментальных методов можно условно разделить на четыре группы
1. Пассивный эксперимент в природе. Наиболее общая задачача, решаемая с привлечением пассивных экспериментов, является определение объема потерь, переноса или накопления грунта в зависимости от факторов эрозии. В эту группу отнесены методы наблюдения и измерения, которые не сопровождаются вмешательством в естественный ход процессов и не оказывают влияния на конечный результат этих процессов. Степень "вмешательства" в естественное течение изучаемых процессов изменяется от метода к методу.
2. Активный эксперимент в природе. К этой группе отнесены методы наблюдения и измерения, использование которых предполагает активное вмешательство исследователя в целях создания искусственных условий, благоприятных для хода процесса в природе или для его видоизменения. При изучении ветровой эрозии также применяют метод активного эксперимента в натурных условиях.
3. Физическое моделирование.
3.1. К первой группе методов относятся:
· метод реперов для оценки смыва грунта и для оценки переотложения грунта по поверхности поля в процессе дефляции;
· метод повторного нивелирования для целей определения потерь грунта от эрозии и дефляции;
· методы измерения мутности воды в ручейках при снеготаянии;
· методы измерения переноса грунта песко-пылеуловителями во время пыльных бурь;
· фотограмметрический метод определения потерь грунта от эрозии и дефляции и т.д.
3.2. Типичным примером методов второй группы является метод стоковых площадок, позволяющий оценить противоэрозионную эффективность разных, главным образом, агротехнических мероприятий. Метод стоковых площадок является комплексным методом. Он включает непрерывное измерение стока (твердого и жидкого), осадков, физических свойств грунта, почвозащитной роли растительности на ограниченном участке склона в течение продолжительного времени.
3.3. Физическое моделирование применяют с целью изучения в лабораторных условиях частично или полностью не изученных физических процессов. К преимуществам методов физического моделирования относится возможность углубленного изучения механизма процессов и роли отдельных факторов эрозии. К недостаткам относиться известная трудность перенесения результатов лабораторных опытов на натуру. Единственной возможностью ее преодоления является обеспечение максимально возможного подобия процессов в модели и натуре. Оно достигается при соблюдении требований подобия:
· геометрического (для выполнения этого требования достаточно добиться того, чтобы модель-оригинал и модель-образ были геометрически подобны),
· кинематического (для выполнения этого требования необходимо обеспечить пропорциональность скоростей и ускорений и одинаковое их направление относительно границ, в геометрически подобных моделях),
· динамического (для выполнения этого требования необходимо добиться пропорциональности и однонаправленности сил, действующих в сходственных точках моделей).
Кинематического и динамического подобия можно достичь только при соблюдении геометрического подобия. Для того, чтобы соблюсти геометрическое подобие, необходимо обеспечить постоянство масштаба всех линейных характеристик (в том числе характеристик шероховатости) модели и натуры. Под масштабами понимают отношение между одноименными величинами натуры (![]() ) и модели (
) и модели (![]() ): (
): (![]() ) — геометрический масштаб, (
) — геометрический масштаб, (![]() ) — масштаб скорости и т.д. Масштабы необходимы при создании, исследовании и интерпретации физической модели, т. е. с их помощью рассчитывают сами модели и переносят результаты моделирования на натуру. Свобода выбора масштаба ограничена системой уравнений, описывающих моделируемое явление. Движение изотермических потоков вязкой несжимаемой жидкости с различными, но постоянными плотностями и вязкостями, описывается системой дифференциальных уравнений (уравнения Стокса и уравнение неразрывности) и соответствующими им начальными и граничными условиями. Переменные, входящие в эти уравнения, являются
) — масштаб скорости и т.д. Масштабы необходимы при создании, исследовании и интерпретации физической модели, т. е. с их помощью рассчитывают сами модели и переносят результаты моделирования на натуру. Свобода выбора масштаба ограничена системой уравнений, описывающих моделируемое явление. Движение изотермических потоков вязкой несжимаемой жидкости с различными, но постоянными плотностями и вязкостями, описывается системой дифференциальных уравнений (уравнения Стокса и уравнение неразрывности) и соответствующими им начальными и граничными условиями. Переменные, входящие в эти уравнения, являются
размерными величинами: ![]() – время,
– время, ![]() – характерный размер (длина),
– характерный размер (длина), ![]() – скорость,
– скорость, ![]() – давление,
– давление, ![]() – объемная сила (в случае сил веса
– объемная сила (в случае сил веса ![]() , т.е. вектору ускорения силы тяжести).
, т.е. вектору ускорения силы тяжести).
По определению два потока являются подобными, если в сходственных пространственно-временных точках области их движения они отличаются между собой только масштабами перечисленных величин, описывающих эти потоки. Если перечисленные размерные переменные в дифференциальных уравнениях нормировать некоторыми постоянными значениями указанных переменных, то безразмерные дифференциальные уравнения, граничные и начальные условия и другие условия единственности решения этих уравнений станут одинаковыми для подобных потоков жидкости. В эти безразмерные дифференциальные уравнения входят безразмерные выражения, которые называют «числами подобия». Они одинаковы для двух подобных потоков:
![]() – число Струхала, (95)
– число Струхала, (95)
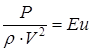 – число Эйлера, (96)
– число Эйлера, (96)
![]() – число Рейнолъдса, (97)
– число Рейнолъдса, (97)
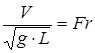 – число Фруда. (98)
– число Фруда. (98)
Кроме масштабов потоков в эти "числа" входят и физические постоянные потоков: ![]() – плотность потока,
– плотность потока, ![]() – кинематическая вязкость потоков. Если в постановке задачи моделирования содержатся сведения о потоках, достаточные для составления какого-либо из приведенных чисел подобия, оно становится критерием подобия. Перечисленные условия подобия являются необходимыми условиями. Установление достаточных условий подобия упирается в необходимость строгого доказательства теоремы о существовании и единственности решений уравнений Стокса для конкретной задачи, что сделано лишь для простейших случаев. Поэтому в общем случае подобные потоки должны были бы отвечать одновременно всем четырем критериям. Однако на практике составить все четыре критерия подобия не представляется возможным, так как не все величины, вводимые при составлении безразмерных уравнений и граничных и начальных условий, описывающих потоки, могут быть заданы заранее. Значения некоторых из них могут быть получены только после того, как будет найдено единственное решение поставленной задачи. Поэтому на практике удается добиться лишь частичного подобия. Поскольку полного динамического подобия добиться практически невозможно, среди действующих в модели сил следует выбрать наиважнейшую и пренебречь другими, слабо влияющими на изучаемое явление.
– кинематическая вязкость потоков. Если в постановке задачи моделирования содержатся сведения о потоках, достаточные для составления какого-либо из приведенных чисел подобия, оно становится критерием подобия. Перечисленные условия подобия являются необходимыми условиями. Установление достаточных условий подобия упирается в необходимость строгого доказательства теоремы о существовании и единственности решений уравнений Стокса для конкретной задачи, что сделано лишь для простейших случаев. Поэтому в общем случае подобные потоки должны были бы отвечать одновременно всем четырем критериям. Однако на практике составить все четыре критерия подобия не представляется возможным, так как не все величины, вводимые при составлении безразмерных уравнений и граничных и начальных условий, описывающих потоки, могут быть заданы заранее. Значения некоторых из них могут быть получены только после того, как будет найдено единственное решение поставленной задачи. Поэтому на практике удается добиться лишь частичного подобия. Поскольку полного динамического подобия добиться практически невозможно, среди действующих в модели сил следует выбрать наиважнейшую и пренебречь другими, слабо влияющими на изучаемое явление.
В таком случае говорят о частичном динамическом подобии и определяют критерии подобия для частных случаев. На частицу потока действуют силы разной природы. Их результирующая равна силе инерции. Каждое из приведенных чисел подобия учитывает одну из действующих сил и силу инерции:
· число Эйлера — силу давления,
· число Рейнольдса — силу вязкости,
· число Фруда — силу тяжести,
· число Струхала — силы, вызывающие автоколебания в потоке.
Приближенное моделирование по одному критерию возможно, если известно, что влияние других значительно слабее. При слабой зависимости изучаемого явления от того или иного критерия говорят об автомодельности относительно этого критерия.
На основе значений критериев подобия можно определить соотношение между масштабами различных величин, обеспечивающее подобие оригинала и модели.
Если для двух сравниваемых потоков известны какие-либо масштабы и физические константы потока и количество их достаточно для составления каких-либо из перечисленных выше чисел подобия, то эти числа становятся уже критериями подобия. Если они для сравниваемых потоков равны, то эти потоки подобны. Количество критериев подобия меньше, чем количество чисел подобия. Это обусловлено тем, что не все масштабы, вводимые при составлении безразмерных уравнений и граничных и начальных условий, описывающих поток, могут быть заданы заранее. Значения некоторых из них могут быть получены только после того, как будет найдено единственное решение поставленной задачи.
Следовательно, метод подобия можно использовать для целей моделирования тогда, когда известны дифференциальные уравнения, описывающие поток. И, если числа подобия для сравниваемых потоков равны, то это означает, что сравниваемые потоки подобны. Полнота подобия, следовательно, зависит от полноты описания этих потоков привлеченными для этих целей дифференциальными уравнениями.
| Предыдущая |
