В.А. Тарбаев, Р.Р. Гафуров Р., Л.М. Хончева
Геодезия с основами землеустройства
Учебно-методическое пособие. Саратов: Саратовский ГАУ, 2009. — 67 с.

4.Вычисление площади землепользования на землеустроительном плане

4.1. Способы определения площадей

Площади угодий на землеустроительном плане можно определить аналитическим, графическим и механическими способами

Самый точный способ вычисления площадей основан на использовании координат вершин участка, определяемых по результатам полевых измерений и математической обработки длин линий и углов между ними (аналитический способ).

Вычисление площади участка по координатам производится по формулам:

т.е. удвоенная площадь землепользования равна сумме произведений каждой абсциссы на разность ординат последующей и предыдущей точек.

Результаты вычислений по этим формулам взаимно контролируются. В процессе вычислений разности контролируются тем, что суммы их равны нулю.

Таблица 6

Вычисление площади землепользования по координатам

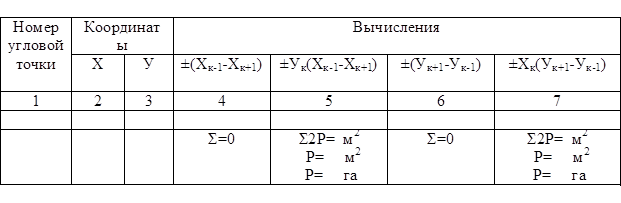
Алгебраические суммы чисел в 4-й и 6-й графах должны быть равны нулю, а в 5-й и 7-й – равны между собой. Эти равные суммы выражают удвоенную сумму площади землепользования.

При вычислении площади графическим способом (см.: Маслов А.В., Юнусов А.Г., Горохов Г.И. Геодезические работы при землеустройстве: Учебное пособие для вузов. М.: Недра, 1990. – 215 с., п.29, С.65) участки изображенные на плане, разбивают на простейшие геометрические фигуры (треугольники, трапеции, прямоугольники, квадраты). Чем больше углов имеет граница землепользования, тем меньше точность вычисления площадей отдельных фигур, а значит и всего землепользования.

Площадь землепользования, вычисленную графически сравнивают с аналитической, она не должна отличаться от аналитической на величину допустимой невязки:

,                       (8)

где f – допустимая невязка;

Р_ан – площадь участка землепользования по координатам (аналитический способ);

М – масштаб.

,                                    (9)

где Р_треуг – площадь участка землепользования, подсчитанная по треугольникам (графический способ).

Элементы, измеряемые в простейших фигурах для вычисления их площадей, показаны на рисунке 13.

Измерив в масштабе плана величины, необходимые для определения площади – основание, высоту, параллельные стороны, определяют площадь каждой геометрической фигуры и затем берут их сумму.

1. Для треугольника (рис. 13,а)

,           (10)

где а, b, с – длины сторон;

h – высота;

c – угол между сторонами а и b треугольника;

р – полупериметр, р=1/2 (а+b+с);

2. Для параллелограмма (рис. 13,б)

           Р=аh                 (11)

3. Для трапеции (рис. 13,в)

           (12)

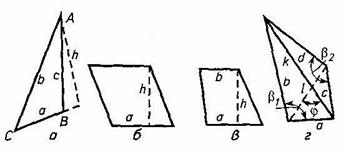
Рис.13. Элементы, измеряемые в простейших фигурах  для вычисления их площади

4. Для четырехугольника (рис. 13,г)

,           (13)

где L и К – диагонали;

 – угол между диагоналями.

Чтобы проконтролировать результаты определения площади, необходимо повторить вычисления, меняя исходные данные. Все вычисления вести как показано в таблице 7, занося туда длины линий, определяемые по плану.

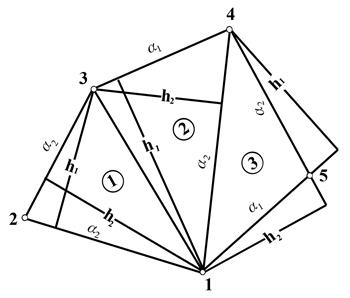
Рис. 14. Разбивка полигона на фигуры при определении площади графическим способом

Например, в треугольнике (рис. 14) можно измерить две высоты h₁=145м и h₂=168 м и две стороны на которые они опущены а₁=540 м и а₂=465 м.

Таблица 7