М.В. Горшков
Экологический мониторинг
Учебное пособие. – Владивосток: Изд-во ТГЭУ, 2010. – 313 с.
| Предыдущая |
Содержание статьи:
Практикум
Тема 3. Биологический мониторинг и оценка интегральных экологических показателей
3.2. Оценка биологического разнообразия сообществ
Для подготовки к заданиям раздела требуется повторить раздел 10.2 курса лекций. Здесь же мы более подробно рассмотрим методы оценки разнообразия экосистем. Самым распространённым до сих пор является определение мер разнообразия (реже используются двойственные им меры концентрации (однородности).
Рассмотрим пример. На некоторой пробной площадке произрастает: 4 берёзы, 4 дуба, 2 клёна и 2 тополя. Всего 16 деревьев. Используем меру Шеннона:
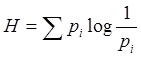 ,
,
где pi – это доли обилия каждого вида в сообществе. Теоретически Н-функция принимает максимальное значение тогда, когда имеет место полная выравненность распределения, что соответствует наибольшей сложности систематической структуры. В нашем случае:
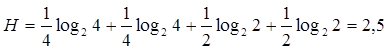 .
.
Для данного сообщества индекс Шеннона меняется от 0 до 4 (для кажого списка верхняя граница индекса может меняться).
Задача №19. Определить индекс Шеннона для видового списка водных беспозвоночных организмов в ручье «Канальном» (Московская область) по обилию: водный ослик – 6, бокоплав – 6, водный скорпион – 4, личинка ручейника в домике – 6, жук тинник – 4, личинка мошки – 3, личинка комара звонца – 6, личинка жука плавунца окаймлённого – 1, волосатик – 4, личинка жука плавунца sp. – 3, личинка равнокрылой стрекозы – 2, малая ложноконская пиявка – 6, моллюск лужанка речная – 1, двухстворчатый моллюск горошина – 4, жук пёстрый гребец – 2, паук доломедес – 1, жук гребляк – 1, моллюск физа – 1, моллюск катушка сплюснутая – 2, паук серебрянка – 1, клоп большой гладыш – 1, жук плавунчик – 3, моллюск прудовик малый – 2, моллюск дрессена – 1, планария – 1, двухстворчатый моллюск шаровка – 1, жук вертячка – 2.
Более сложным является сравнительный анализ таксономического состава сообществ. В курсе лекций (раздел 10.2) мы уже рассматривали общую схему сравнительного анализа по детерминистской схеме.
Для более глубокого понимания анализа рассмотрим гипотетический пример. В таблице 3.1 имеется 5 площадок с 8 возможными видами (первичная матрица типа объект/признак), в которой отмечено присутствие/отсутствие видов на пробных площадках:
Таблица 3.1
Матрица данных гипотетического примера
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
1 |
1 |
1 |
1 |
1 |
|
2 |
0 |
1 |
0 |
0 |
1 |
|
3 |
1 |
1 |
1 |
1 |
1 |
|
4 |
1 |
1 |
1 |
1 |
1 |
|
5 |
0 |
0 |
1 |
1 |
1 |
|
6 |
0 |
0 |
0 |
0 |
1 |
|
7 |
0 |
0 |
1 |
1 |
0 |
|
8 |
0 |
0 |
0 |
0 |
0 |
Далее проведём анализ видовой структуры гипотетического сообщества. Для начала рассчитаем матрицу пересечений (в нашем случае позволяет увидеть общее число видов и число общих видов для сравниваемых объектов):
Таблица 3.2
Матрица пересечений гипотетического примера
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
3 |
3 |
3 |
3 |
3 |
|
2 |
3 |
4 |
3 |
3 |
4 |
|
3 |
3 |
3 |
5 |
5 |
5 |
|
4 |
3 |
3 |
5 |
5 |
5 |
|
5 |
3 |
4 |
5 |
5 |
7 |
Напоминаем, что матрица симметрична относительно диагонали. Оцениваем разнородность диагональных элементов. Они одновелики (перепады значений незначительны), следовательно можно применять меры сходства. Для иллюстрации методов сравнительного анализа мы также рассчитаем и матрицу мер включения (как вам уже известно, данная матрица является наиболее информативной относительно степени сходства биологических объектов):
Таблица 3.3
Матрица мер включения гипотетического примера (в %)
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
100 |
100 |
100 |
100 |
100 |
|
2 |
75 |
100 |
75 |
75 |
100 |
|
3 |
60 |
60 |
100 |
100 |
100 |
|
4 |
60 |
60 |
100 |
100 |
100 |
|
5 |
43 |
57 |
71 |
71 |
100 |
В нашем случае наблюдается очень большое сходство между площадками. При пороге в 100% 1 площадка включается в площадки 2-5, 2 площадка в 5 площадку, 3 площадка в 4-5, 4 в 3 и 5. Представьте эти отношения в виде ориентированного графа и оцените банальность/оригинальность видовых списков. Методом симметризации рассчитаем матрицу мер сходства Сёренсена (напомним, что эта матрица является двойственной матрице мер различия (расстояний), т.е. мера сходства является дополнением до единицы матрицы различия).
Таблица 3.4
Матрица мер сходства Сёренсена гипотетического примера (в %)
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
100 |
87,5 |
80 |
80 |
71,5 |
|
2 |
87,5 |
100 |
67,5 |
67,5 |
78,5 |
|
3 |
80 |
67,5 |
100 |
100 |
85,5 |
|
4 |
80 |
67,5 |
100 |
100 |
85,5 |
|
5 |
71,5 |
78,5 |
85,5 |
85,5 |
100 |
Определим кластеры с помощью метода арифметического среднего (рис 3.1). Для этого просматривая ячейки сверху вниз и слева направо, ищем максимальное значение сходства (кроме диагональных элементов).
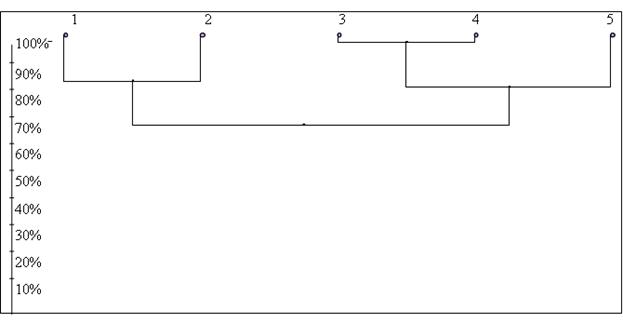
Рисунок 3.1. Дендрограмма, построенная методом среднего арифметического связывания (мера сходства Сёренсена)
Находим на пересечении 3 и 4 площадки 100%. Это наш первый кластер [3, 4]. Все значения матрицы, которые пересекаются с элементами нового кластера пересчитываем как среднее арифметическое этих значений. Например, K1,3=80, K1,4=80, следовательно среднее арифметическое также будет равно 80 (K1[3,4]=80). Аналогично определяем следующие кластеры. Рассчитайте самостоятельно и постройте дендрограмму. Последовательно получим: кластер [1, 2] = 87,5; кластер [[3,4],5] = 85,5. Объединение кластеров происходит на уровне сходства – 74%.
Лабораторная работа №4.
Цель: использование схемы сравнительного анализа для оценки видовой структуры сообществ.
Объект изучения: видовые списки сообществ.
Оборудование и материалы: Требуется максимально полно оценить видовую структуру данного сообщества и сделать соответствующие выводы. За основу берём типовые матрицы пересечения (см. Приложение).
| Предыдущая |
