М.В. Горшков
Экологический мониторинг
Учебное пособие. – Владивосток: Изд-во ТГЭУ, 2010. – 313 с.

Практикум

Тема 2. Статистическая обработка экологических результатов

2.5. Дисперсионный анализ

Что делать, когда мы хотим сравнить несколько выборок? Попарно сравнивать параметрическими или непараметрическими критериями? Очень быстро мы утонем в расчётах. Но, разумеется, наука уже знает способ нам помочь. Для сравнения трёх и более выборок используют дисперсионный анализ (ANOVA).

Дисперсионный анализ, основы которого были разработаны Фишером в 1920-1930 гг., позволяет устанавливать не только степень одновременного влияния на признак нескольких факторов и каждого в отдельности, но также их суммарное влияние в любых комбинациях и дополнительный эффект от сочетания разных факторов. Разумеется, и в этом случае остается масса неучтенных факторов, но, во-первых, методика позволяет оценить долю их влияния на общую изменчивость признака, а во-вторых, исследователь обычно имеет возможность выделить несколько ведущих факторов и исследовать именно их воздействие на изменчивость признаков.

Дисперсионный анализ позволяет решить множество задач, когда требуется изучить воздействие природных или искусственно создаваемых факторов на интересующий исследователя признак. Дисперсионный анализ принадлежит к числу довольно трудоемких биометрических методов, однако правильная организация опыта или сбора данных в природных условиях существенно облегчает вычисления.

Идея дисперсионного анализа заключается в разложении общей дисперсии случайной величины на независимые случайные слагаемые, каждое из которых характеризует влияние того или иного фактора или их взаимодействия. Последующее сравнение этих дисперсий позволяет оценить существенность влияния фактора на исследуемую величину. Таким образом, задача дисперсионного анализа состоит в том, чтобы выявить ту часть общей изменчивости признака, которая обусловлена воздействием учитываемых факторов, и оценить достоверность делаемого вывода.

Пусть, например, А – исследуемая величина,  – среднее значение величины А, учитываемые факторы мы обозначим буквой х, неучитываемые – z, а все факторы вместе – буквой у (или припиской этих букв к соответствующим символам). Неучитываемые факторы составляют «шум» – помехи, мешающие выделить степень влияния учитываемых факторов. Отклонение А от  при действии факторов х и z можно представить в виде суммы

(А-)=У=Х+Z,

где Х – отклонение, вызываемое фактором х, Z – отклонение, вызываемое фактором z, У – отклонение, вызываемое всеми факторами. Кроме того, предположим, что Х,У,Z – являются независимыми случайными величинами, обозначим дисперсии через s²_Х, s²_Y, s²_Z, s²_А. Тогда имеет место равенство:

s²_А=s²_Х+s²_Z

Сравнивая дисперсии можно установить степень влияния факторов х и z на величину А, т.е. степень влияния учтенных и неучтенных факторов.

Непременным условием дисперсионного анализа является разбивка каждого учитываемого фактора не менее чем на две качественные или количественные градации. Если исследуется влияние одного фактора на исследуемую величину, то речь идет об однофакторном комплексе, если изучается влияние двух факторов – то о двухфакторном комплексе и т.д. Для проведения дисперсионного анализа обязательным условием является нормальное распределение и равные дисперсии совокупности случайных величин.

Для пояснения логической схемы дисперсионного анализа рассмотрим простейший произвольный пример. Предположим, что совокупности возрастающих доз удобрения на разных делянках имеют нормальное распределение и равные дисперсии. Имеется m таких совокупностей (разные делянки), из которых произведены выборки объемом n₁,n₂,…,n_m. Обозначим выборку из i-ой совокупности через (х_i1,х_i2,…х_in) — урожайность делянок. Тогда все выборки можно записать в виде таблицы, которая называется матрицей наблюдений.

Таблица 2.3

Матрица наблюдений однофакторного дисперсионного комплекса

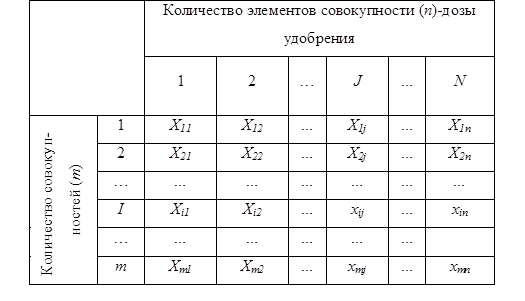
Средние этих выборок обозначим через . Для проверки гипотезы о равенстве средних нулевую гипотезу запишем как , альтернативную в виде .

Гипотеза Н₀ проверяется сравнением внутригрупповых и межгрупповых дисперсий по F-критерию. Если расхождение между ними незначительно, то нулевая гипотеза принимается. В противном случае нулевая гипотеза отвергается и делается заключение о том, что различия в средних обусловлено не только случайностями выборок, но и действием исследуемого фактора.

Для изучаемого признака характерно три типа изменчивости:

1. Факториальная (или групповая) изменчивость. Характеризуется тем, что для каждой из совокупностей имеется своя средняя арифметическая (). Разница в средних зависит, очевидно, от разного действия факторов;

2. Остаточная изменчивость. Характеризуется различными значениями признака внутри каждой градации. Эти различия не зависят от влияния фактора. Видимо, их причина лежит вне опыта, определяется неучитываемыми в данном анализе факторами.

3. Общая изменчивость. Заключается в том, что все наблюдения дисперсионного комплекса отличаются друг от друга (или иногда совпадают).

Мерой изменчивости признака в выборке служит сумма квадратов отклонений его значений от средней арифметической . Эта величина, отнесенная к числу наблюдений, дает меру рассеяния, именуемую дисперсией, которая и применяется в дисперсионном анализе.

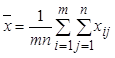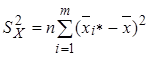1. Мерой факториальной изменчивости будет сумма квадратов отклонений средних значений групп () от общего среднего : . Эту величину иногда называют рассеиванием по факторам.

2. Мера остаточной изменчивости выразится суммой квадратов отклонений всех наблюдений в данной совокупности от среднего значения совокупности: .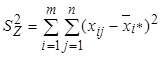

3. Мерой общей изменчивости является сумма квадратов отклонений в дисперсионном комплексе от общего среднего: .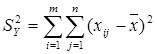

Тогда в соответствии с основной идеей дисперсионного анализа можно записать: S²_y=S²_x+S²_z или:

.

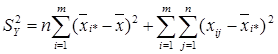Вычислим факториальную и остаточную дисперсии, как меры соответствующих типов изменчивости признака в дисперсионном комплексе

.

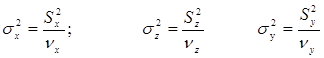В этих формулах фигурируют степени свободы (n_х, n_z, n_у), т.к. дисперсия s² и есть сумма квадратов отклонений в расчете на одну степень свободы. Число степеней свободы есть количество значений, необходимых для восстановления утерянного.

1. Число степеней свободы для факториальной дисперсии равно числу совокупностей без единицы (m-1), т.к. все группы связаны друг с другом лишь одним общим условием – значением средней арифметической всего дисперсионного комплекса ().

2. Число степеней свободы для остаточной дисперсии равно числу наблюдений в комплексе минус число совокупностей (mn—m) ибо все наблюдения связаны наличием в каждой группе своей средней арифметической ().

3. Число степеней свободы для вычисления общей дисперсии всего комплекса равно числу наблюдений в комплексе без единицы (mn—1), ибо все наблюдения связаны только одним общим условием – наличием общей средней ().

Затем необходимо рассчитать доли влияния учтенного и неучтенного факторов как отношения соответствующих сумм квадратов отклонений:

.

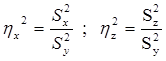Эти величины представляют собой не что иное, как квадраты корреляционных отношений. В сумме эти показатели должны всегда составлять 1 (100%). Теперь можно ответить на интересующий вопрос: насколько учитываемый фактор ответственен за изменчивость результативного признака и сколько процентов падает на долю неучтенных факторов.

Таблица 2.4

Логическая схема однофакторного дисперсионного комплекса

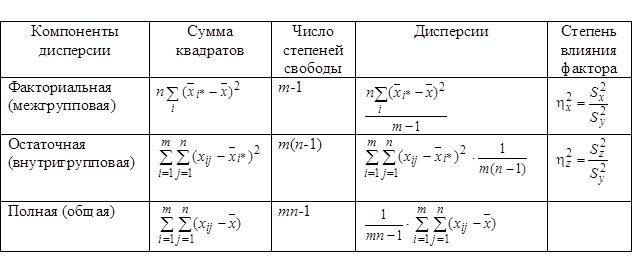
Для проверки достоверности полученного вывода необходимо провести проверку по F-критерию. Определяют значение критерия Фишера (F), представляющего собой отношение двух дисперсий – факториальной и остаточной – 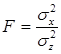 и сравнивают его с табличным в зависимости от числа степеней свободы n₁=m-1 и n₂=mn—m. Для того, чтобы отвергнуть нулевую гипотезу, необходимо, чтобы полученное значение критерия было больше табличного. Однофакторный дисперсионный анализ удобно представить в виде таблицы:

Лабораторная работа №2.

Цель: использование методики однофакторного дисперсионного анализа для определения взаимосвязей.

Объект изучения: урожайность условных полей (см. условие ниже).

Оборудование и материалы: калькулятор.

Предположим, что изучается влияние возрастающих доз удобрения определенного типа на урожайность какой-либо культуры. Пусть имеются четыре дозы удобрения (А₁…А₄, причем А1<A2<A3<A4), которое использовали на пяти делянках по каждой дозе (m=4, n=5). Требуется выяснить: влияет ли повышение дозы удобрения на урожайность и если да, то достоверен ли этот вывод настолько, чтобы можно было рекомендовать этот опыт сельскому хозяйству. Результаты представьте в виде таблице по аналогии с типовым примером Результаты первичных наблюдений приведены в таблице.

Таблица 2.5

Исходные данные для расчета однофакторного дисперсионного комплекса